中学になると勉強がグッと難しくなりますよね。
算数は数学に変わり、よくわからなくなっているという人も多いでしょう。
特に難しいのが比例と反比例ですよね。
正の比例と負の比例の違いもよくわからないという方もいることでしょう。
ここでは中1数学でつまづきやすい比例と反比例について
正の比例と負の比例の身近な例
比例と反比例の日常生活の例をあげながら紹介していきます。
【比例】の身近な例【負の比例・負の相関】の身近な例
まず、普通の比例について考えてみましょう。
比例というのは「一方の数が増えるともう一方の数が増える」という関係です。
式で表すと
となります。
比例の身近な例では『散歩』を考えてみましょう。
自分の歩幅を「50cm」とします。
ということは、1歩歩けば50cm進みますし
100歩歩けば5000cm、つまり50m進むことになりますよね。
このように「歩数」という数が増えるほど
「距離」もどんどん増えていきます。
これが『比例』です。
ちなみにこの例を式で表すと
ということになります。
比例は、グラフにすると右上がりの線になります。
負の比例・負の相関 日常での例「学校までの通学路」
つぎに『負の比例』を考えてみましょう。
負の比例というのは『比例定数が負の数』のことを表します。
負の比例の身近な例として、
例えば『学校までの通学路』を考えてみましょう。
先ほどの散歩の例と同じく、自分の歩幅は50cmとします。
あなたが自宅から学校に向かって50cmずつ歩いていくと、学校まで歩いた距離も増えますね。
「歩数」が増えるほど、「距離」も増える。
これは『正の比例』です。
では、あなたが『学校とは反対方向』へ歩いて行くと、どうなるでしょう?
学校からはどんどん遠ざかっていきますね。
「歩数」が増えるほど、学校まで歩いた距離は『マイナス方向』に増えていく。
そうなると式としては
ということになります。
負の比例は、グラフだと右下がりの線になります。
以上をまとめると、
正の比例と負の比例、この2つの違いを覚えておきましょう。
反比例と負の比例の違いは?「減り方」が違う、「グラフの線」が曲線が直線か
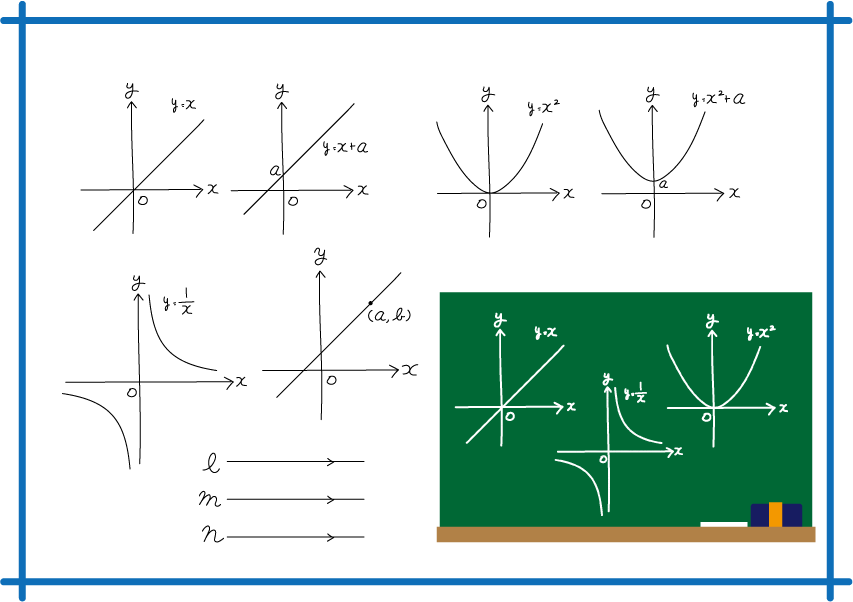
比例と同様にわかりにくいのが『反比例』ですよね。
ここで反比例の前に思い出したいのが、比例の定義です。
比例の場合は「一方の数が増えるともう一方の数が増える」という定義で、「y=ax」という式で表すことができます。
先ほどお見せした、比例の身近な例『通学路』で言うと、
「正の比例」のときは、歩数が増えれば距離は増えていましたよね。
そして「負の比例」で言うと、歩数が増えることによって、負の数も増えていますよね。
一方、反比例の場合は
という定義があります。
反比例と負の比例は、まったく違いますので注意してくださいね。
反比例の式は
という式で表すことができます。
反比例の身近な例として
『おやつのアメをみんなで分ける』を考えてみましょう。
12個のアメがあったとき。
x人に配る場合の、1人あたりのアメの個数(y)を考えてみます。
この場合、式としては
になります。
12個のアメを2人で分けるときは、1人あたり6個のアメになります。
12個のアメを3人で分けるときは、1人あたり4個のアメになります。
12個のアメを4人で分けるときは、1人あたり3個のアメになります。
12個のアメを6人で分けるときは、1人あたり2個のアメになります。
このように反比例の場合は
人数が2倍、3倍となっていくと、
1人あたりのアメの数は1/2倍、1/3倍になります。
また反比例のグラフは『曲線』で描かれるという特徴があります。
アメの例の場合は、人数ですので負の数はありませんが、
負の数まである場合のグラフは『双曲線』と呼ばれる二つの曲線が出来上がります。
数学になると「定義」、「定義の式」「グラフ」というのは非常に大切になります。
ぜひこれらを理解しながら比例や反比例を考えるようにしてくださいね。
まとめ
中1の数学というのは数学の中でも基礎中の基礎です。
これから学年が上がるとどんどん難しくなっていきますし、
わからないところは今のうちにしっかり理解をしておくことが大切です。
その中でもつまづきやすいのが比例・負の比例・反比例ですよね。
これらは定義や定義式、そしてグラフで考えるとわかりやすくなっていきます。
負の比例と反比例もわかりにくいですが、
どちらも定義式に当てはめてグラフを書いてみるとわかりやすくなると思います。
ぜひわからないところはしっかりと理解をして、数学を楽しむようにしてくださいね。







